백준 BOJ 3049 - 다각형의 대각선

https://www.acmicpc.net/problem/3049

3049번: 다각형의 대각선

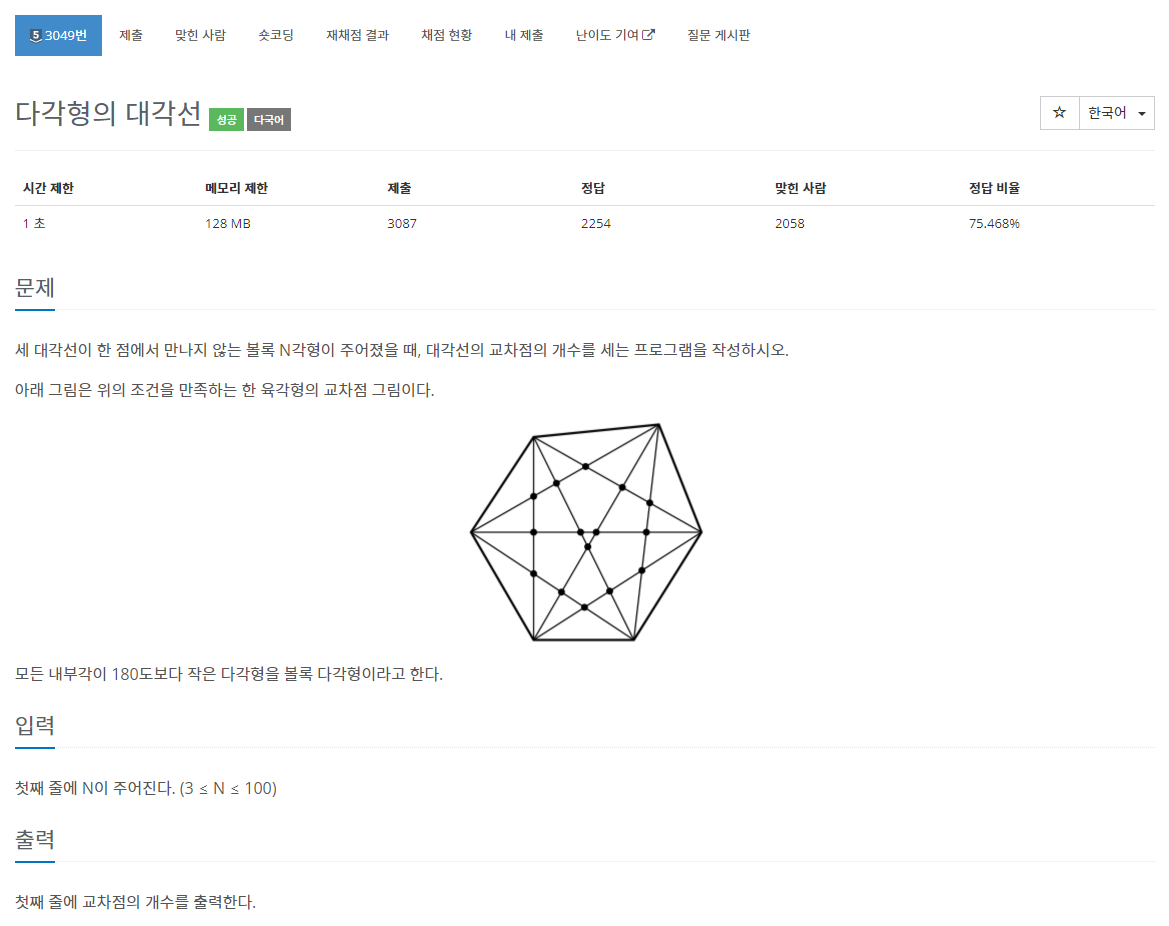
수학문제.

"세 대각선이 한 점에서 만나지 않는" 이라는 조건이 중요하다.

근데 아마 지문이슈가 좀 있는거같은게

N>=3 인 N개의 대각선이 한점에서 만나지 않는 이 좀 더 정확하지 않나 싶다.

 

암튼

세 대각선이 한 점에서 겹치지 않는다면

대각선의 교차점이 생기는 경우는 무조건 두 대각선이 서로 한 점에서 만나는 경우인데,

대각선은 볼록 N각형의 꼭짓점에서 임의의 점 두개를 골라서 만들어 낼 수 있고,

 

대각선 둘이 서로 교차하면서 한개의 점에서 만나려면

문제의 볼록다각형이라는 조건상 반드시 X자 모양으로 만나야 한다.

 

그래서 점 네개를 골라주면 반드시 X자 모양이 되는 경우의 수 단 하나만이 조건에 부합하므로

 

볼록 N각형의 꼭짓점 N개 중에서 임의의 점 네개를 고를 수 있는 경우의 수를 묻는 문제이고,

즉 nC4를 계산해서 출력해주면 정답 되시겠다.

 

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;

ll dp[123][123] = {0};

int nCr(int n, int r){
	if(!n) return 0;
	if(!r) return 1;
	if(n == r) return 1;
	
	if(dp[n][r] != 0) return dp[n][r];
	
	return dp[n][r] = nCr(n-1,r-1) + nCr(n-1,r);
}

int main(){
	int N;
	cin >> N;
	
	ll spot = nCr(N,4);
	
	cout << spot;
	return 0;
}