누가봐도 다익스트라같이 생긴 문제이고,
실제로 다익스트라를 빠삭하게 이해하고 있다면 해결할수 있는 문제였다.
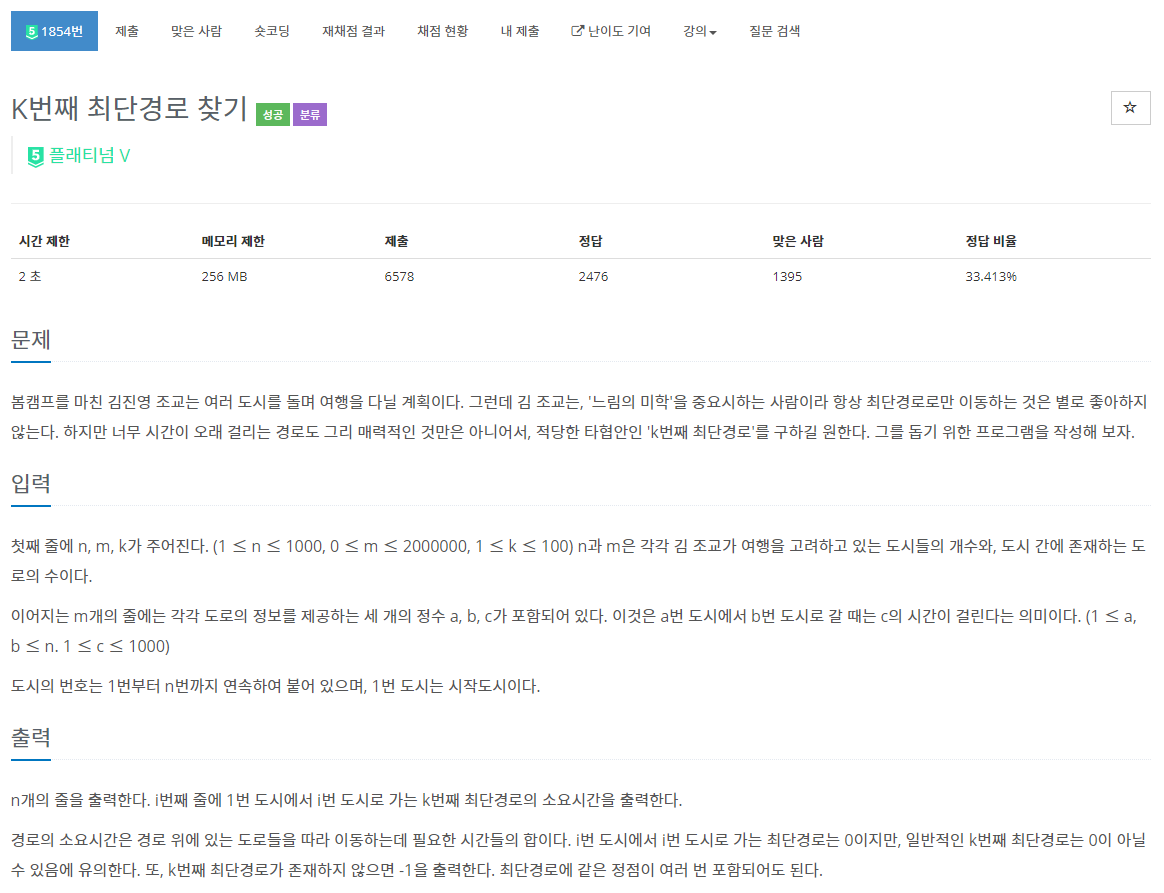
1854번: K번째 최단경로 찾기
첫째 줄에 n, m, k가 주어진다. (1 ≤ n ≤ 1000, 0 ≤ m ≤ 2000000, 1 ≤ k ≤ 100) n과 m은 각각 김 조교가 여행을 고려하고 있는 도시들의 개수와, 도시 간에 존재하는 도로의 수이다. 이어지는 m개의 줄에
www.acmicpc.net
다익스트라는 탐색 도중에서 의도적으로 최단경로가 아닌 경우를 배제하는데,
이 배제되는 경로들을 전부 잘 저장해두고 정리해주면 된다.
if(ans[next].size() < k){
pq.push({-(dist+dis), next});
ans[next].push(dist + dis);
}
else if (ans[next].top() > dist + dis){
ans[next].pop();
ans[next].push(dist + dis);
pq.push({-(dist+dis), next});
}일반 다익스트라에서 다음과 같은 부분이 추가되었는데,
ans배열에 추가된 경로의 수가 K개보다 작아서
경로를 추가해줘야만 하는 경우가 위의 IF문이고,
ans배열에 추가된 경로의 수가 K개를 넘지만,
K번째 최단경로의 가중치를 갱신해줘야 하는 경우가 아래의 else IF문이다.
이 두가지 케이스만 잘 구분해서 작성해주면 AC를 받을 수 있다.
더보기
#include <bits/stdc++.h>
#define INF 123456789
using namespace std;
priority_queue<pair<int,int>> pq;
vector<pair<int,int>> v[1234];
int d[1234] = {0};
int n,m,k;
int a,b,c;
priority_queue<int> ans[1234];
void dijkstra(int node){
for(int i=0; i<1234; i++) d[i] = INF;
d[node] = 0;
ans[node].push(0);
pq.push({0, node});
while(!pq.empty()){
int now = pq.top().second;
int dis = -pq.top().first;
pq.pop();
for(int i=0; i<v[now].size(); i++){
int next = v[now][i].first;
int dist = v[now][i].second;
if(ans[next].size() < k){
pq.push({-(dist+dis), next});
ans[next].push(dist + dis);
}
else if (ans[next].top() > dist + dis){
ans[next].pop();
ans[next].push(dist + dis);
pq.push({-(dist+dis), next});
}
}
}
return;
}
int main(){
scanf("%d %d %d", &n, &m, &k);
for(int i=0; i<m; i++){
scanf("%d %d %d", &a, &b, &c);
v[a].push_back({b,c});
}
dijkstra(1);
//for(int i=1; i<=n; i++) printf("[%d]", d[i]); puts("");
for(int i=1; i<=n; i++){
if(ans[i].size() != k) printf("-1\n");
else printf("%d\n", ans[i].top());
}
return 0;
}
반응형