백준 BOJ 1967 & 1167 - 트리의 지름

제목이 같은 날먹문제...

 

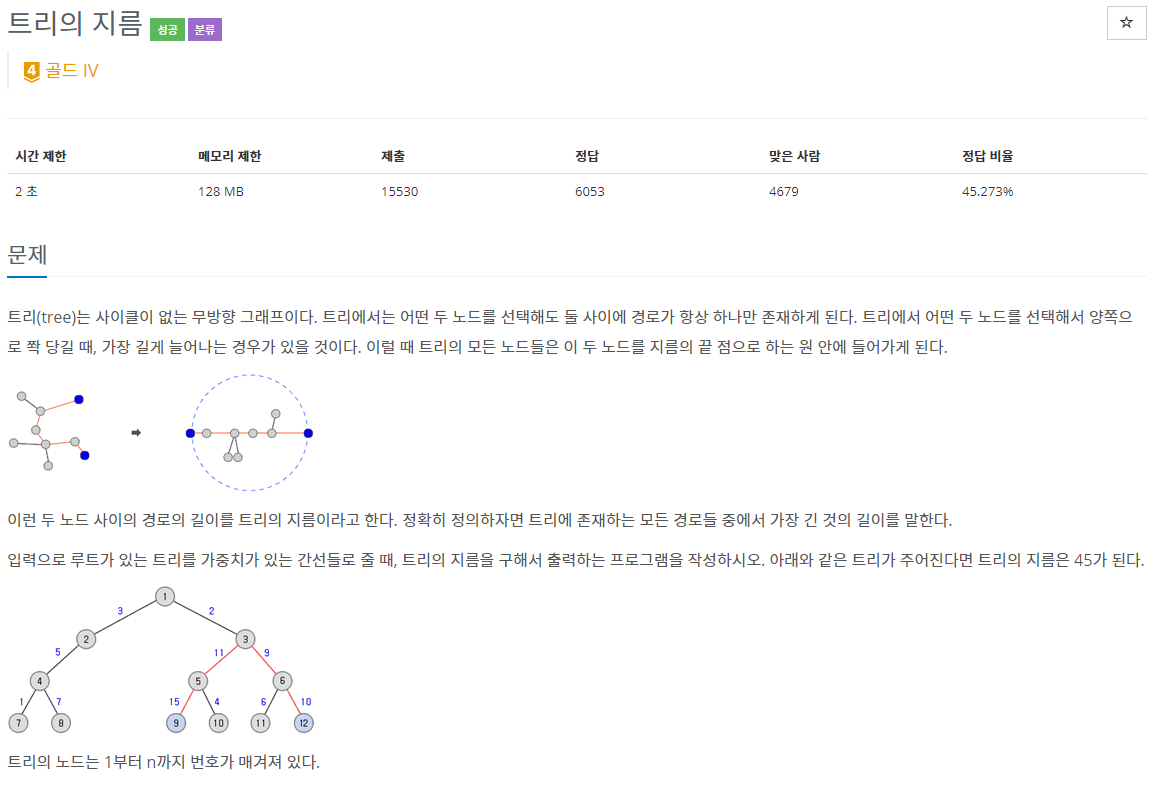
트리에 존재하는 모든 경로 중 가장 긴것의 길이를 찾으라하고 있다.

dfs로 풀었다.

 

일단 가장 긴 경로는 반드시 리프노드 - 리프노드 간 길이일 것이다.

리프노드가 아닌 노드가 긴 경로가 된다면

그 노드의 자식노드로 더 긴 경로가 있을수밖에 없기 때문이다

( 가중치의 길이가 음수가 될 수 없다 )

 

처음 생각한것은 1을 기준으로 가장 긴 경로 & 두번째로 긴 경로 를 찾는 것인데,

중복문제도 있고, 그림에서처럼 1을 지나지 않는 가장 긴 경로도 있기에

 

일단 루트노드에서 가장 긴 경로를 찾고, 그 경로에서 나온 리프노드를 시작점으로하는

가장 긴 경로를 찾아주었다.

 

루트노드에서 가장 긴 경로와

실제 가장 긴 경로가

1 ) 하나도 겹치지 않는다면 조건에 모순이 생기고,

2 ) 겹친다면 가중치가 중복이어서 가장 긴 경로가 두개 이상 생기는 경우이므로

정답을 구해줄 수 있다.

 

자세한 증명은 아랫분이 깔끔하게 해주셨다.

blog.myungwoo.kr/112

트리의 지름 구하기

 

따라서, DFS/BFS 를 두번 돌려주면 문제가 해결된다.

1167 트리의 지름

#include <bits/stdc++.h>
using namespace std;

vector<pair<int,int>> g[123456];
int vis[123456] = {0};

int maxv; // max value
int maxn; // max node

int dfs(int node, int dis){
	for(int i=0; i<g[node].size(); i++){
		int next = g[node][i].first;
		int dist = g[node][i].second;
		
		if(vis[next]) continue;
		vis[next] = true;
		
		if(dis+dist > maxv){
			maxv = dis + dist;
			maxn = next;
		}
		dfs(next, dist+dis);
	}
	return 0;
}

int main(){
	int n;
	int a,b,c;
	scanf("%d", &n);
	
	for(int i=0; i<n; i++){
		scanf("%d", &a);
		while(1){
			scanf("%d", &b);
			if(b == -1) break;
			scanf("%d", &c);
			g[a].push_back({b,c});
			g[b].push_back({a,c});
		}
	}
	
	memset(vis, 0, sizeof(vis));
	vis[1] = 1;
	dfs(1,0);
	
	memset(vis, 0, sizeof(vis));
	vis[maxn] = 1;
	dfs(maxn, 0);
	
	printf("%d", maxv);
	return 0;
}

 

1967 트리의 지름

#include <bits/stdc++.h>
using namespace std;

vector<pair<int,int>> g[123456];
int vis[123456] = {0};

int maxv; // max value
int maxn; // max node

int dfs(int node, int dis){
	for(int i=0; i<g[node].size(); i++){
		int next = g[node][i].first;
		int dist = g[node][i].second;
		
		if(vis[next]) continue;
		vis[next] = true;
		
		if(dis+dist > maxv){
			maxv = dis + dist;
			maxn = next;
		}
		dfs(next, dist+dis);
	}
	return 0;
}

int main(){
	int n;
	int a,b,c;
	scanf("%d", &n);
	for(int i=0; i<n-1; i++){
		scanf("%d %d %d", &a, &b, &c);
		g[a].push_back({b,c});
		g[b].push_back({a,c});
	}
	
	memset(vis, 0, sizeof(vis));
	vis[1] = 1;
	dfs(1,0);
	
	memset(vis, 0, sizeof(vis));
	vis[maxn] = 1;
	dfs(maxn, 0);
	
	printf("%d", maxv);
	return 0;
}

입력 조건만 바뀐 문제이니

하나만 풀어도 두개를 날먹할수있다