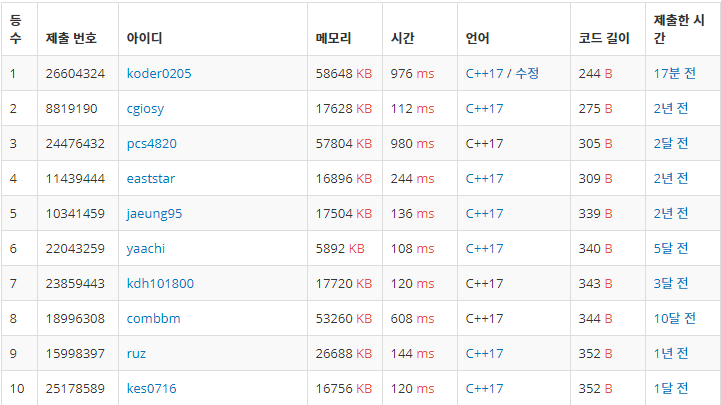
특이한 풀이가 있어
쉬운 난이도인 실버 2임에도 불구하고 블로그 글을 써보려 한다.
원래 정해는 이제 최대공약수를 이용하는 풀이법이다.
최대공약수로 i 와 j를 나눠주면, 이 두가지 수가 이제 마치 "기약분수" 처럼 보이게 되고,
이를 통해 중복을 제거해줄수 있다.
하지만 여기서 기약분수라는 저 느낌을 잘 활용하면 소스코드의 길이를 대폭 줄일 수 있다.
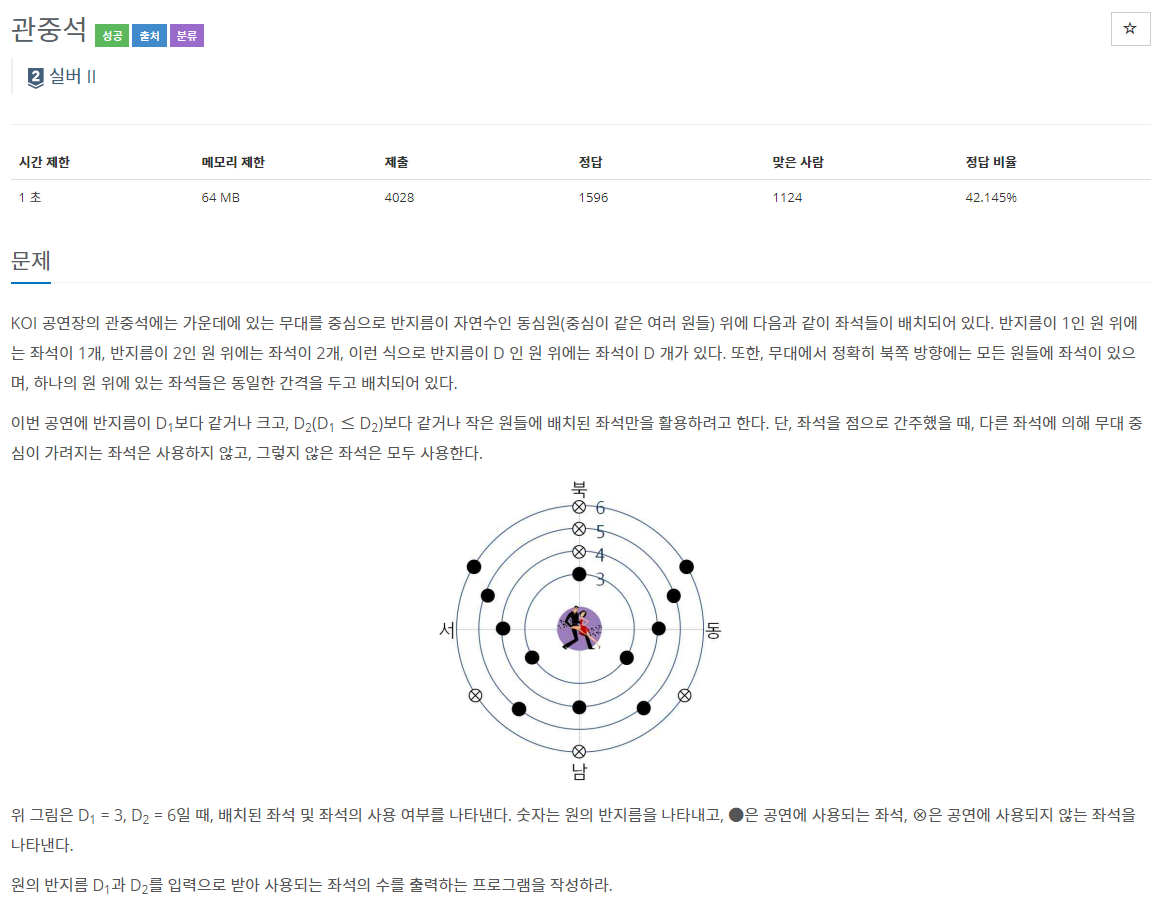
10166번: 관중석
KOI 공연장의 관중석에는 가운데에 있는 무대를 중심으로 반지름이 자연수인 동심원(중심이 같은 여러 원들) 위에 다음과 같이 좌석들이 배치되어 있다. 반지름이 1인 원 위에는 좌석이 1개, 반지
www.acmicpc.net
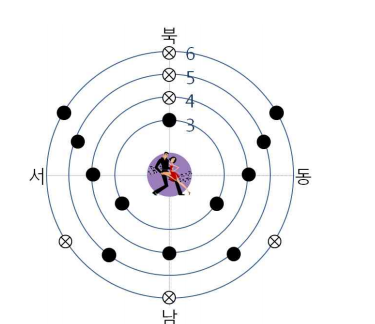
고등학교 2학년 교육과정에 라디안 각을 배우게 되는데,
이때 각도는 2*π 가 360도와 대응되게 된다.
이와 비슷한 느낌으로 360도를 숫자 1에 대응시키면
모든 위치들을 0과 1 사이 숫자에 할당시켜줄 수 있다.
그리고 이 위치들은 정확히 같은 각도만큼을 떨어져 있으므로
반지름이 K인 원 위의 점들은 1/K 만큼의 각도 차이로 떨어져서 존재한다.
근데 컴퓨터에서 나눗셈을 계산할때는
2/6 이나 1/3 을 모두 같이 0.333333..... 으로 나타내기 때문에, 알아서 기약분수꼴
로 변환을 해주는 것이랑 비슷한 것이다.
그렇기 때문에 저 1/K, 2/K, 3/K .... K/K 를 전부 셋에 insert 해주면
알아서 중복이 삭제되고,
따라서 셋의 전체 크기인 s.size()가 해답이 된다.
#include <bits/stdc++.h>
using namespace std;
set<double> s;
int main(){
int d1, d2;
scanf("%d %d", &d1, &d2);
for(int i=d1; i<=d2; i++){
for(int j=1; j<=i; j++){
s.insert((double)j/i);
}
}
printf("%d", s.size());
return 0;
}여담
C++17 에서는 셋을 활용한 풀이가 몇개 없는듯 하다.
솔직히 공백제거도 안하고
숏코딩의 트릭처리도 전혀 하지 않았는데
이게 왜 C++17 숏코딩 순위에 올라있는지 잘 이해가 안간다...