처음 보고 뇌절왔었던 문제
ㄹㅇ 고등부 넘모 어려워요 ㅠㅠ
20192번: 순서 섞기
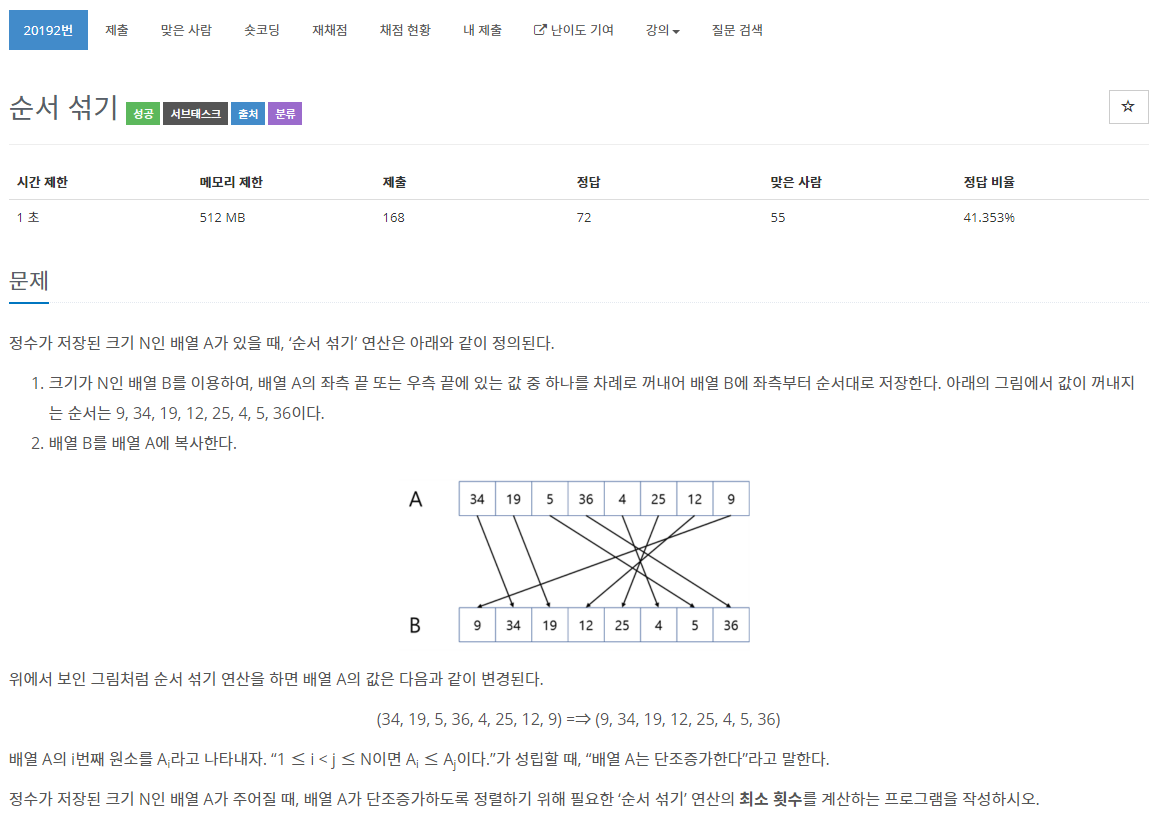
정수가 저장된 크기 N인 배열 A가 있을 때, ‘순서 섞기’ 연산은 아래와 같이 정의된다. 크기가 N인 배열 B를 이용하여, 배열 A의 좌측 끝 또는 우측 끝에 있는 값 중 하나를 차례로 꺼내어 배열 B
www.acmicpc.net
처음에는 걍 그리디 + 구현인줄알았다 ( 정올 준비용으로 티어 끄고 풀어서 )
그래서 간단히 짜고 제출했더니 아니나다를까 TLE.
생각해보니 본선 2번인데 구현으로 풀릴리가 없지
어케풀지 한참 고민하고 있는데
뭔가 정렬 비슷하단 생각이 들어서
정렬관련한것들을
인터넷에서 좀 뒤져봤다.
머지소트가 ↗↗의 형태로 주어진 입력을 합쳐 ↗ 하나로 만드는 정렬이더라.
이거보고 바로 삘이 왔다.
문제에서 제시하고 있는 정렬방법은↗↘ 을 합쳐 ↗로 만드는 방법이기 때문이다.
어째서 이렇게 말할수 있는가 하면
머지소트를 할때는
포인터를 두개를 만들고
둘다 화살표의 꼬리부분부터 시작해서
둘이 비교해보고 포인터를 증가시킨다.
그런데 입력으로 주어진것은 ↘를 거꾸로 거슬러 올라가면
머지소트랑 똑같은 방법으로 비교한다는것을 관찰할 수 있고,
이는 테스트케이스 2를 통해서도 볼 수 있다.
이제 모든 입력을 ↗와 ↘두개로 분별해줄 수 있게 된다.
이렇게 해서 나누어진 다음
케이스를 나눠서 머리를 굴려줬다.
1) ↗↘↗↘형태
이경우는 ↗(↗↘)↘로 봐 주면
바깥 ↗↘를 ↗로, 안쪽을 역정렬해서 ↘ 로 만들어주면
↗↘↗↘ => ↗↘ => ↗이 된다.
2) ↗↘↗형태
이 경우 역시 잘 정리해주면 ↗↘ => ↗ 이 된다.
3) ↘↗형태
이 경우에는 이제 역순으로 정렬을 해서 ↘을 먼저 만들어준 다음
이걸 반대로 뒤집어서 ↗을 만들어줄 수 있다.
이렇게 대략적으로 거의 모든 형태에 대한 값을 구할 수 있었고,
1번 형태를 확장한 규칙을 보다가 log2의 값을 구해주면 되겠다 싶었다.
log2(1) = 0이고 log2(2) = 1 이니
주어진 테스트케이스 두개에서 log2()에 들어갈 값
K = (화살표의 갯수) 라는것을 알 수 있었고,
이 K의 갯수를 세면 되는
간단한 문제로 바뀐다.
#include <bits/stdc++.h>
using namespace std;
int in[345678] = {0};
int main(){
int n;
scanf("%d", &n);
int cnt = 1;
int updown=1; // 1 => up, 0 => down
for(int i=1; i<=n; i++){ scanf("%d", &in[i]); }
for(int i=2; i<=n; i++){
if(updown==1){ if(in[i-1] > in[i]) { updown = 0; cnt++; } }
else { if(in[i-1] < in[i]) { updown = 1; cnt++; } }
}
//printf("[%d]", cnt);
printf("%d", (int)ceil(log2(cnt)));
return 0;
}
updown이 화살표의 방향을 기억하고 있다가, 기존 화살표와 비교방향이 달라지면 화살표방향을 바꿔준다.
사실 bits/stdc++.h가 비표준이라 쓰기 싫긴 했는데
math니 뭐니 찾기 너무 귀찮았다....
