통신교육 문제 겸 백준에도 있길래
날먹했다
나이스
단순한 이진탐색인데
맞왜틀을 왜이렇게 많이 했는지 모르겠고
AC받긴 했지만 솔직히 WA코드랑 뭔차인지도 잘 모르겠지만
proofed by AC기법으로 증명되었기에
여기다 써본다.
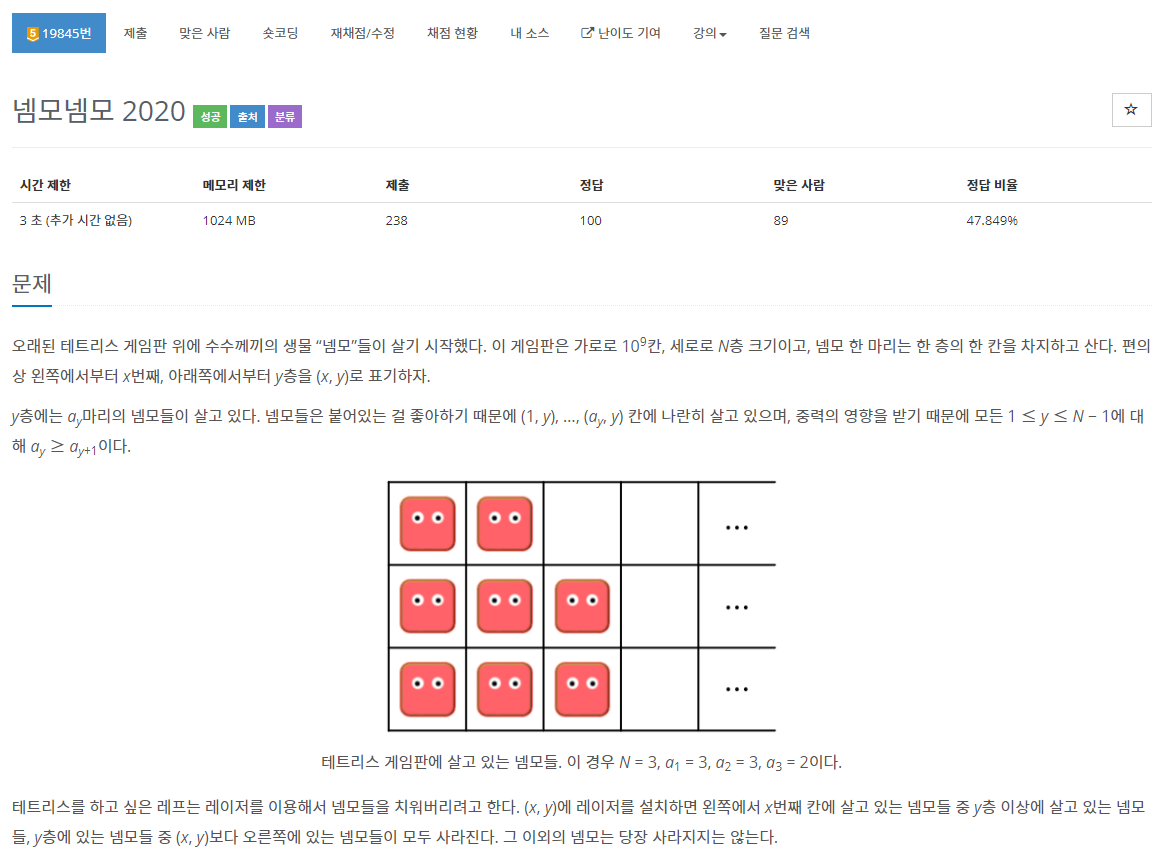
19845번: 넴모넴모 2020
오래된 테트리스 게임판 위에 수수께끼의 생물 “넴모”들이 살기 시작했다. 이 게임판은 가로로 109칸, 세로로 N층 크기이고, 넴모 한 마리는 한 층의 한 칸을 차지하고 산다. 편의상 왼쪽에서부
www.acmicpc.net
search 함수는 전형적인 이분탐색 함수이다.
그냥 적당히 짰다.
nemo는 혹시몰라 엄청 넉넉하게 만들어뒀는데
솔직히 필요없을거같다
#include <stdio.h>
#include <algorithm>
using namespace std;
int nemo[543210] = {0};
int search(int k, int s, int e){
int mid;
while(s<e){
mid = (s+e)/2;
if(nemo[mid] >= k){ s = mid + 1; }
else{ e = mid; }
}
return s;
}
int main(){
int n,q;
int res;
int tmp;
int x,y;
scanf("%d %d", &n, &q);
for(int i=1; i<=n; i++) scanf("%d", &nemo[i]);
for(int i=0; i<q; i++){
scanf("%d %d", &x, &y);
if(nemo[n] >= x) res = 1;
else res = 0;
tmp = search(x,1,n);
if( nemo[y]-x <0 || tmp-y <0 ) printf("0\n");
else printf("%d\n", res + nemo[y]-x + tmp-y);
}
return 0;
}첫번째로 뇌절친 파트
어떨때는 1을 더하고, 어떨때는 빼야하는데
수많은 그림을 그려본 결과 찾고자 하는 값이 입력된 넴모넴모들의 최솟값보다 작으면
+1을 해줘야 했다.
res = 1과 res = 0은 그걸 구분해주고 있고,
시간아끼려고 tmp변수 만들어서
함수는 한번만 호출했다.
가로줄은 nemo[y]-x, 세로줄은 tmp-y로 깔끔하게 나타낼 수 있는데,
여기서 하나의 유의점은 수가 음수가나오는경우 둘중 한곳에서만 나와도
무조건 0을 출력해야한다는 것이다.
처음에 max(0, nemo[y]-x) + ... 식으로 접근했는데
아마 그래서 틀리지 않았을까?

반응형